[블로깅 챌린지] Data Structure - 배열, 리스트, 스택

1장

자료구조 :

일련의 동일한 타입의 데이터(ex-배열)를 정돈하여 저장한 구성체

    -배열, 리스트, 스택, 큐, 트리 등

 

For what? : 데이터에 대해 탐색, 삽입, 삭제 등의 연산을 효율적으로 하려고

 

데이터 + 데이터에 관련된 연산 이 둘을 함께 고려해야 한다.

 

배열(Array): 동일한 타입의 원소들 → “연속적“인 메모리 공간에 할당

각 항목 → 하나의 원소에 저장

int[] a = new int[10];
String[] s = new String[10];
Student[] st = new Student[100];

// 데이터타입[] 배열 이름 = new 데이터타입[배열크기]; 의 형식이다.

 

추상 데이터 타입(ADT): 데이터 + 데이터에 대한 추상적인 연산들

 

추상이란?: 구체적인 세부 명세(연산을 어떻게 구현해야 하는지)가 없는 것

 

*자료구조 = 추상 데이터 타입을 구체적(실제 프로그램)으로 구현한 것

    → ADT == java interface

    → 자료구조 == java class

 

데이터 타입과 연산에 대한 일반적인 명세(어떤 연산인지만)만 존재

     → 그 연산들이 어떻게 실행되는지는 제공 X

 

 

데이터 추상화

 

데이터와 연산을 독립적으로 구현될 수 있도록 별도의 캡슐화

 

 

수행 시간 분석

 

for 자료구조의 효율성 측정 (알고리즘의 효율성 계산 방식과 동일하다)

 

    -시간 복잡도: 수행 시간

    -공간 복잡도: 알고리즘이 수행되는 동안 사용되는 메모리의 크기

대부분은 시간 복잡도만 사용한다.

 

 

시간 복잡도

 

연산 실행 동안 사용된 기본 연산 횟수 → 입력 크기의 함수로 표현

    기본 연산

        -데이터 간 크기 비교

        -데이터 리딩

        -데이터 갱신

        -단순한 계산(단순 연산)

 

4종류의 분석이 있다.

 

    -최악경우 분석

        어떤 입력에 대해서라도 만족하는 최대 소요 시간(Upper bound)

    -평균경우 분석

        입력의 확률 분포 가정, 균등분포(Uniform Distribution) 사용

    -최선경우 분석

        가장 빠른 수행 시간 분석; 최적(Optimal) 알고리즘 탐색에 사용

    -상각 분석(Amortized Analysis)

        일련의 연산을 수행하여 총 연산횟수를 합함

            → 이를 연산횟수로 나눔

 

일반적으로 최악경우 분석으로 표현한다.

 

 

상각분석

 

“N회의 연산을 수행한 총 시간 / N“ = 1회 연산의 평균 수행 시간이다. 참고로, 입력의 확률분포에 대한 가정이 필요없다!

    → 최악경우 분석보다 매우 정확한 분석 가능

 

상각분석이 가능한 알고리즘 = 오래 걸리는 연산 + 짧게 걸리는 연산

    → 뒤섞여서 수행되는 공통점을 가진다

 

수행시간의 점근표기법

다항식으로 표현되며, 이를 입력의 크기에 대한 함수로 표현하기 위해 점근표기법 사용한다.

    Big-Oh 표기법

    Big-Omega 표기법

    Theta 표기법

이 있다.

 

순차 탐색

 

선형 탐색 또는 직렬 탐색이라고도 한다.

주어진 목표 값을 찾아 리스트를 앞에서부터 순차적으로 탐색한다

목표가 발견된 첫 번째 위치 리턴하고, 목표가 발견되지 않으면 음수를 리턴함

    O(Big-Oh)표기법

        정의: 모든 N≥N_0 에 대해서 f(n)≤cg(N)이 성립하는 양의 상수 c와 N_0이 존재하면 f(N) = O(g(N))이다.

        의미: N_0과 같거나 큰 모든 N(즉, N_0이후의 모든 N)에 대해 f(N)이 cg(N)보다 크지 않다는 것.

        “f(N) = O(g(N))” : N_0보다 큰 모든 N에 대해서 f(N)이 양의 상수를 곱한 g(N)에 미치지 못한다는 것을 의미

        g(N) = f(N)의 Upper Bound

            -O(1) = 상수시간

             -O(log N) = 로그(대수)시간

             -O(N) = 선형시간

             -O(N log N) = 로그선형시간

             -O(N^2) = 제곱시간

             -O(N^3) = 세제곱시간

             -O(2^N) = 지수시간

         증가율이 작은 것 부터 순서대로 나열한 Big-O표기법의 종류이다.

 

 

순환

 

메소드의 실행 과정 중 스스로를 호출하는 것

 

팩토리얼과 조합을 계산하기 위한 식의 표현이다.

    무한한 길이의 숫자 스트림 만들기

    분기하여 자라는 트리 자료구조

    Fractal

등에 기본 개념으로 사용된다.

 

메소드가 자기 자신을 호출할 때 무한 호출을 방지하기 위해 Base조건을 만들어둔다.

    If 무한 호출 발생 → StackOverFlowError가 발생한다.

    If문을 사용하여 Base조건에 도달했는지 체크하고, 이때를 기준으로 순환을 멈추는 방식으로 작성해야 한다.

 

순환으로 구현된 메소드는 두 부분으로 구성된다.

    Base case : 앞서 말한 Base조건에 해당하는 케이스

    순환 case : 스스로를 호출하는 부분(recursion 연산이 발생)

일반적으로 recursion은 가독성만 높지, 메모리 사용 측면에선 반복이 더 좋다.

다만 반복으로 표현하기 어렵고 recursion이 더 쉬운 경우도 있다.

 

 

2장

 

단순 연결 리스트: 동적 메모리 할당을 받아 노드(Node)를 저장하고, 노드는 레퍼런스를 이용하여 다음 노드를 가리키도록 구성하였다. → 노드들을 한 줄로 연결한 구조가 됨

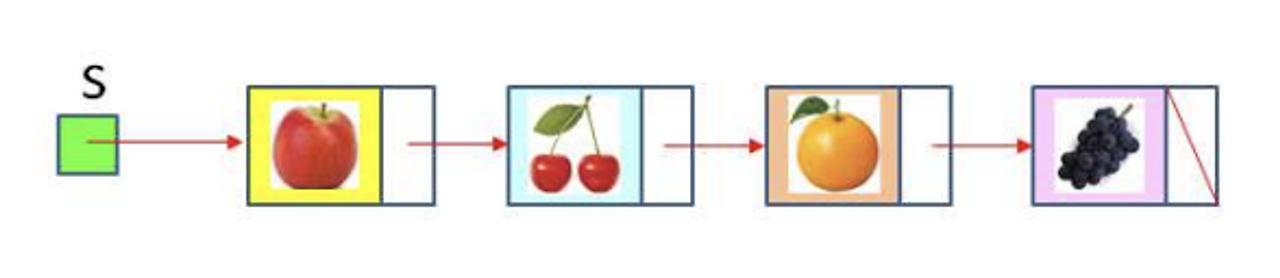
• 연결 리스트에서는 삽입이나 삭제 시 다른 노드들의 이동이 필요 없다.
• 배열 = 처음부터 배열의 크기를 정해야 함 → 빈 공간이 존재하게 됨
• 연결 리스트에서는 탐색하려면 항상 첫 노드부터 원하는 노드까지 차례대로 다 방문해야함

 

public class Node<E> {
	private E item;
	private Node<E> next;
	public Node(E newItem, Node<E> node) {
		item = newItem;
		next = node;
	}
	
	public E getItem() {
		return item;
	}
	public Node<E> getNext() {
		return next;
	}
	public void setItem(E newItem) {
		item = newItem;
	}
	public void setNext(Node<E> newNext) {
		next = newNext;
	}
}

E는 노드가 가리키는 값이고 Node<E>는 노드로, E를 가리키는 역할이다.

 

완성된 SList 는 아래와 같다.

import java.util.NoSuchElementException;

public class SList<E> {
	protected Node head;
	private int size;
	public SList() {
		head = null;
		size = 0;
	}
	public int search(E target) {
		Node p = head;
		for (int k=0; k<size; k++) {
			if (target == p.getItem()) {
				return k;
			}
			p = p.getNext();
		}
		return -1;
	}
	public void insertFront(E newItem) {
		head = new Node(newItem, head);
		size++;
	}
	public void insertAfter(E newItem, Node p) {
		p.setNext(new Node(newItem, p.getNext()));
		size++;
	}
	public void deleteFront() {
		head = head.getNext(); // head에 head 다음 노드를 바로 할당시킴으로써 기존의 head 값을 덮어씌움
		size--;
	}
	public void deleteAfter(Node p) {
		Node t = p.getNext();
		p.setNext(t.getNext());
		t.setNext(null); //null로 놓으면 t가 setNext로 가져올 것은 null로 해버려서 더 이상 다른 노드와 연결되어 있지 안다는 것을 의미함 ... t가 가리키는 next를 null로 설정한 것.
		size--;
	}
	public void print() {
		Node<E> current = head;
		while (current != null) {
			System.out.print(current.getItem() + "\t");
			current = current.getNext();
		}
	}
	public int size() {
		return size;
	}
}

 

Node<E>에서의 E는 노드가 가리키는 값을 가상으로 지칭하는 역할을 한다. 그리고 SList에서는 Node(newItem, head)를 사용하여 head에 값을 넣어주는 방식을 사용한다.

 

이중 연결 리스트 : 각 노드가 2개의 레퍼런스를 가지고 각각 이전 노드와 다음 노드를 가리키는 거

 

기존의 단순 연결 리스트 : 삽입/삭제 시 이전 노드를 가리키는 레퍼런스를 알아야 하고, 역방향으로 탐색이 불가하였음.

이를 이중 연결 리스트에서는 보완하였으나, 각 노드마다 추가 메모리를 사용한다는 단점이 생김

public class DList<E> {
	protected DNode head, tail;
	protected int size;
	public DList() {
		head = new DNode(null, null, null); //(null, null, tail)이라 쓰지 않고 아래에 head.setNext(tail);으로 작성한 이유 - 아직 tail을 정의하지 않은 포지션이기 때문이다.
		tail = new DNode(null, head, null);
		head.setNext(tail);
		size = 0;
	}
	
	public void insertBefore(DNode p, E newItem) {
		DNode t = p.getPrevious();
		DNode newNode = new DNode(newItem, t, p);
		p.setPrevious(newNode);
		t.setNext(newNode);
		size++;
	}
	public void insertAfter(DNode p, E newItem) {
		DNode t = p.getNext();
		DNode newNode = new DNode(newItem, p, t);
		p.setNext(newNode);
		t.setPrevious(newNode);
		size++;
	}
	public void delete(DNode x) {
		DNode f = x.getPrevious();
		DNode r = x.getNext();
		f.setNext(r);
		r.setPrevious(f);
		size--;
	}
	public void print() {
		if(size == 0) {
			System.out.println("리스트 비어있음");
		}
		DNode<E> current = head;
		while(current != tail) {
			if(current.getItem() != null) {
				System.out.print(current.getItem() + "\t");
			}
			current = current.getNext();
		}
		System.out.println();
	}
}